Bounding the Softmax
TL;DR: This post explores methods for calculating lower and upper bounds on the softmax function’s output and discusses why this is crucial for neural network verification.
Many neural network architectures rely on the softmax function, such as the transformer which uses it in the attention layer, or merely as an output layer to generate a probability-like output. The verification of neural networks field has mostly stayed away from such networks, in part due to the difficulties raised by the use of the softmax. Verification methods often use a bound propagation procedure in which bounds over the input of the network are propagated through each layer of the network. As the naive bounds of the softmax are relatively loose, the bounds become unusable after a small amount of layers as the looseness compounds upon itself. However, with architectures using the softmax becoming more prevalent, there has been work in increasing the tightness of these bounds. Three papers that have formulated tighter bounds for the softmax, which I summarise here alongside a summary of softmax and its uses.
The Softmax Function
There are two main crucial properties of the softmax function that make it useful in neural networks. The first is that it transforms the input (e.g. the logits of a classifier) into a probability-like distribution in that the output sums to one. This makes the output interpretable as a probability distribution over independent classes. The second is that it is differentiable, which is crucial for backpropagation. This property allows the model to calculate gradients and update weights during the training process.
For input $x \in \mathcal{R}^{K}$ the output $p$ of the softmax is given by:
\[p_j = \frac{e^{x_j}}{\sum_{j'=1}^{K} e^{x_{j'}}} = \frac{1}{1 + \sum_{j' \neq j} e^{x_{j'} - x_j}}, \quad j = 1, \ldots, K.\]Interactive visualisations in 1D and 2D [1] highlight interesting properties of the softmax function. For example, adding a constant to each input does not change the output probabilities, and scaling the inputs affects the ‘spread’ or ‘temperature’ of the probabilities.
A notable application of the softmax function, denoted as $\sigma$, is in the attention mechanism of transformers, where it helps model interactions between different elements of the input:[2]
\[\sigma \left( \frac{X W_Q W_K^{\top} X^{\top}}{\sqrt{d_k}} \right) X W_V\]Recent Advancements in Softmax Bounds
Approach 1: Composite Operations [3]
Shi et al. (2019) decompose the softmax into constituent operations that can each be linearly bounded sequentially, with the bounds of each operation passed to the next. Specifically they:
- Bound the sum of exponentials. Each exponential is bounded from above by the chord between the endpoints (the upper and lower bounds from the previous layer), and from below by a tangent to the exponential.
- Bound the reciprocal. This is also a convex function of a scalar and so the lower and upper bounds are obtained by just minimising the lower bound from the sum of exponentials, and maximising the upper bound.
- Bounds on the softmax. The final bounds are obtained by composing the two above bounds.
Approach 2: Composite Operations [4]
Wei et al. (2023) reformulate the previous composition by instead taking the logarithm of the softmax and exponentiating this. They then approach this in a composite approach as before.
- They take the exponential itself as the lower bound and a chord between the lower and upper inputs as the upper bound.
- The log-sum-exponential function (LSE) is concave and therefore can be used as the upper bound. The lower bound is more challenging as it is a multivariate function. They provide two different approaches with different strengths and weaknesses. The advantage of the first formulation is that the inputs tend to be on the flatter part of the exponentials, leading to less loss when bounded by the chords. The disadvantage is that the chords used as bounds tend to be over intervals that are wider.
- Bounds on the softmax. The bounds on the softmax are again obtained by composing the two above.
- The above are non-linear bounds, which is an issue for symbolic interval propagation. Using the fact that any tangent plane to a convex lower bound is also a sound lower bound, and any tangent to an upper bound is a sound upper bound, they linearise their obtained bounds. The difference here between the bounds of Shi et al. (2020) and these, are these only linearise once, rather than after each constituent operation.
Shown below are the bounds on the softmax (with 2 inputs) for the linear bounds, exponential reciprocal (Shi et al.) and log-sum-exp bounds.
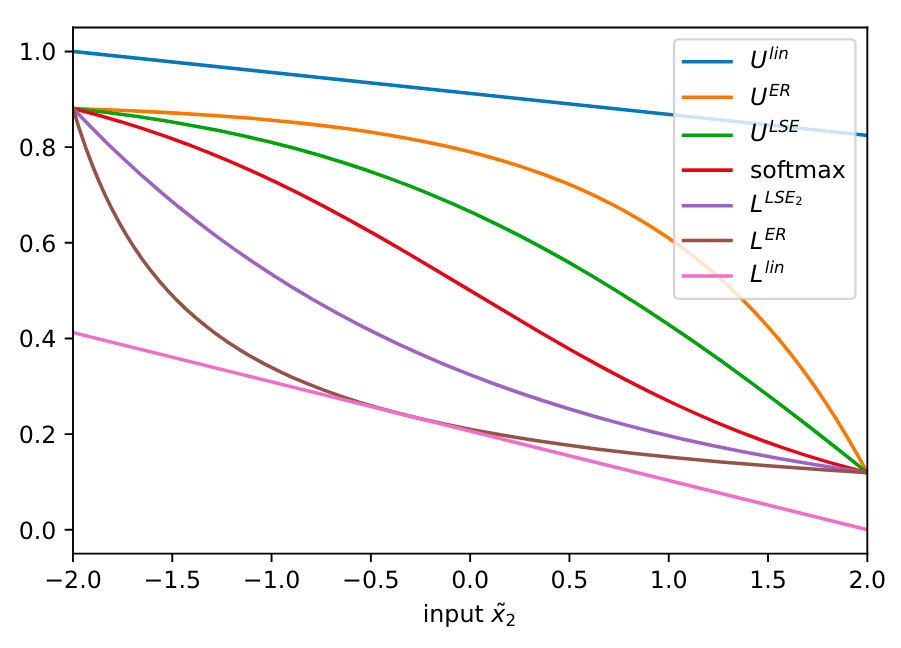
In their experiments they use a with outputs that have differing amounts of probability concentrated on only one component. The left/right columns in the figure below refer to the upper/lower bounds on the softmax output, whilst the top/bottom rows are the case where the output shown is the component with high/low concentration.
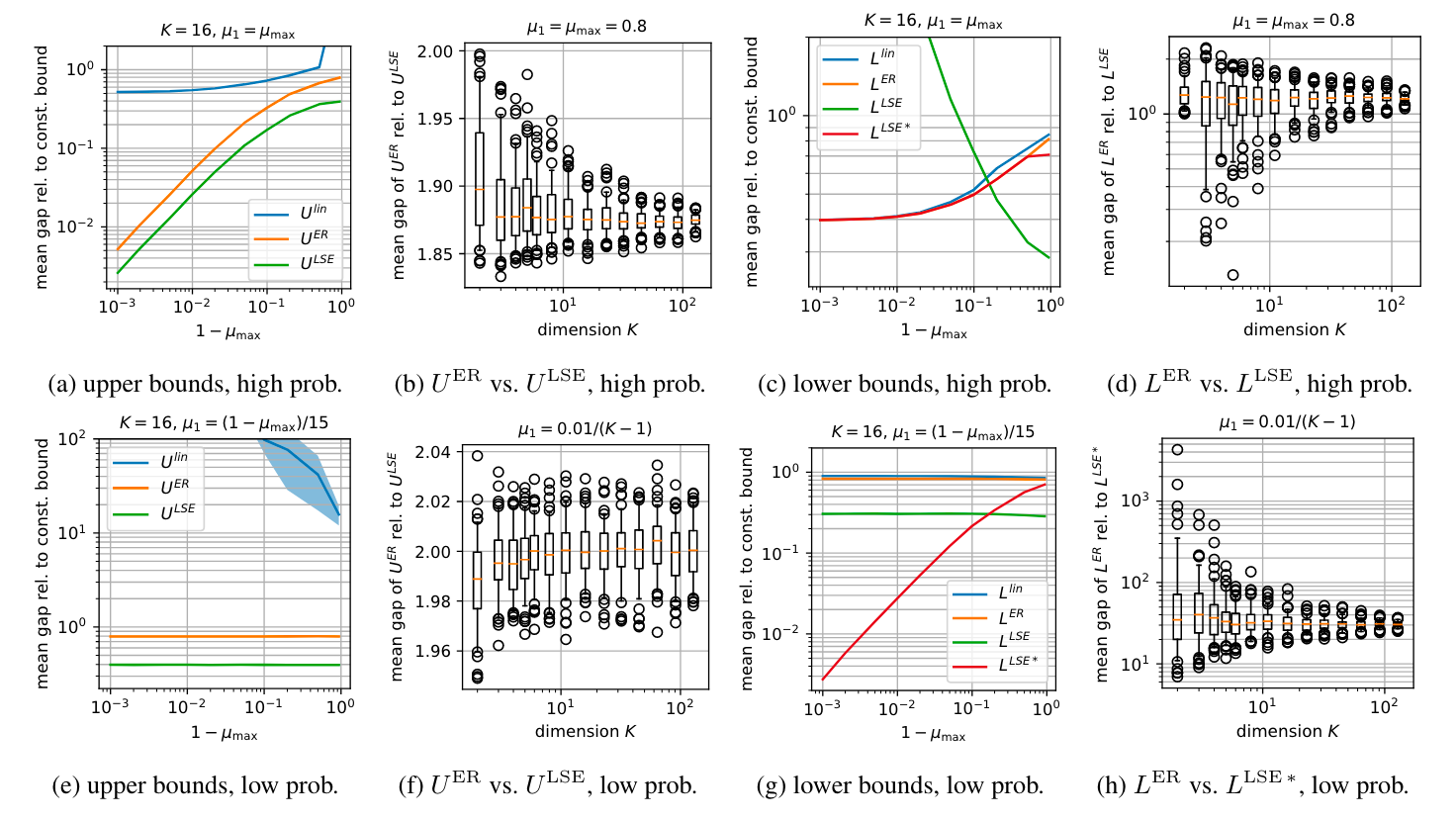
Approach 3: Accounting for dependencies [5]
This approach is based on the insight that prior works ignore dependencies among the inputs of the softmax. The authors call it the $n$-dimensional relation approach and claim it achieves 3.24 times larger certified radii compared to the state-of-the-art. This approach does not decompose the softmax into simple functions and relax them sequentially, which they state causes errors in earlier relaxations to adversely affect subsequent stages. Instead, to circumvent this impact they adopt one-stage relaxations that treat softmax as an $n$-dimensional function without decomposition.
Conclusion
By providing more precise bounds, these methods may allow bound propagation based verification methods to incorporate the softmax function, and hence be used on popular architectures such as transformers.
References
[1] Elliot Whaite, Softmax Function Explained In Depth with 3D Visuals, Youtube.
[2] Vaswani et al., Attention is All you Need, NeurIPS, 2017.
[3] Shi, Z., Zhang, H., Chang, K.-W., Huang, M., & Hsieh, Robustness Verification for Transformers, Shi et al., 2019, International Conference on Learning Representations.
[4] Wei et al., 2023, Convex Bounds on the Softmax Function with Applications to Robustness Verification, Proceedings of The 26th International Conference on Artificial Intelligence and Statistics.
[5] Zhang, Y., Shen, L., Guo, S., & Ji, S. (2024). GaLileo: General Linear Relaxation Framework for Tightening Robustness Certification of Transformers. Proceedings of the AAAI Conference on Artificial Intelligence, 38(19), Article 19.